Transformers

feb 18 2026

Ok so we’ve derived and tested single head attention in the last post. The question now is: what can we tweak to make it better?

When we ran our MLP models we did a basic setup with some guessed hyperparameters and tweaked them until we felt OK that we’d explored a reasonable amount of the search space.

We’re going to follow the same pattern here, but we’re not going to play with hyperparameters quite yet; there’s some more low-hanging fruit if we think about the architecture.

Recall that our architecture looks like this at present:

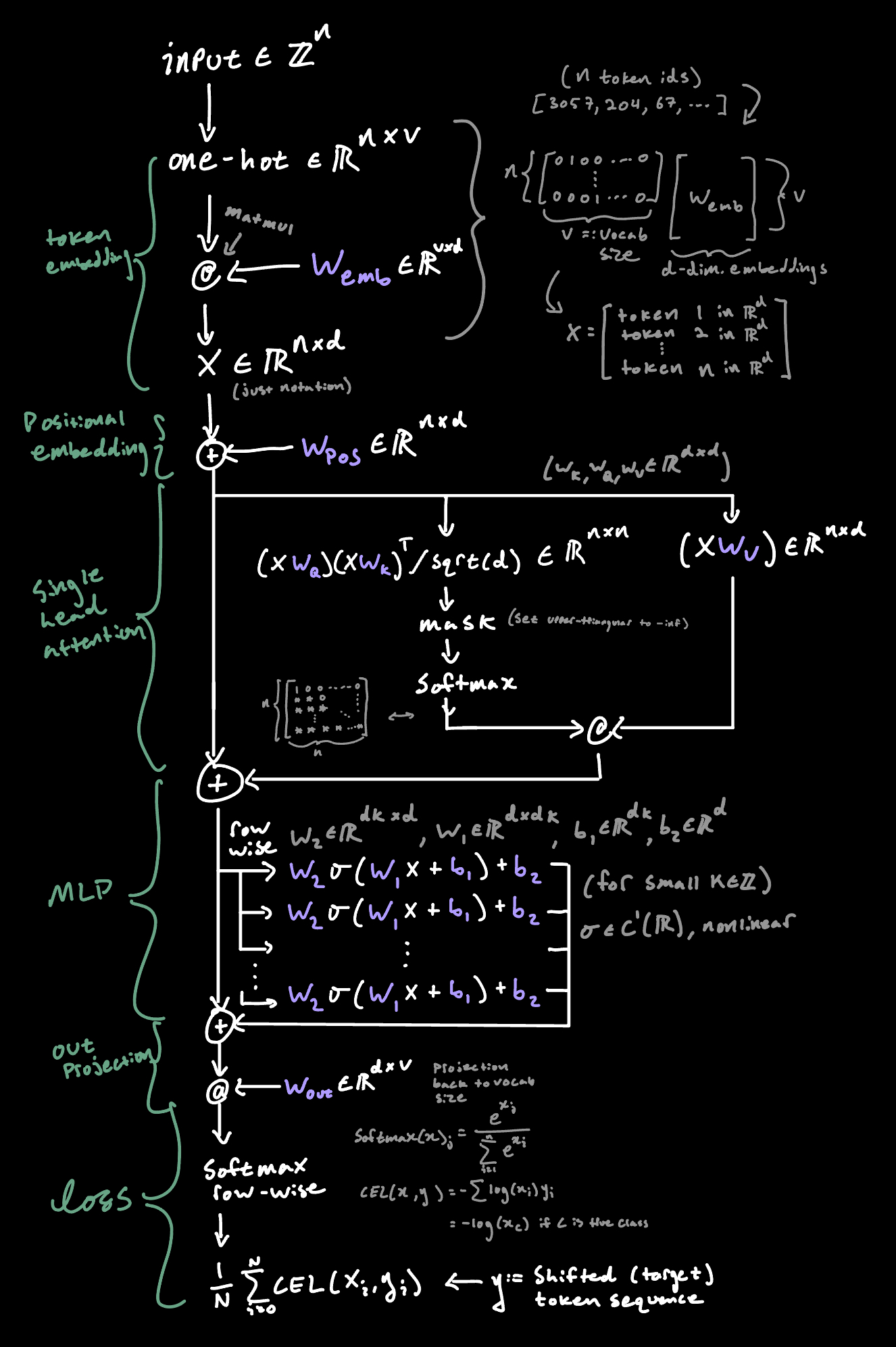
So now the question is: what can we do better?

naive multi head attention

First, let’s think about what the actual attention mechanism is doing. It’s taking in our input, ‘contextualizing’ token \(t_i\) with tokens \(t_{i-k}\) and then returning some ‘delta’ that’s added to our input.

Let’s also get in the habit now of calling the ‘input with stuff added to it as it flows through the network’ the ‘Residual Stream’.

So the attention mechanism is responsible for computing the actual attention mask (the \(n \times n\) shaped \(QK^T\) part), then using that to compute some function of our input (the \(V\) part) which gets added on to the residual stream.

The problem here is that the space where \(X\) is projected via \(W_V\) is responsible for encoding all the things you might want to push onto the residual stream. If we’re looking at a sequence that’s like “things I enjoy: apples, pie, ice cream”, then \(W_V\) is responsible not only for encoding “things following positive words like ‘enjoy’ should get pushed more positively” but also “things following ‘:’ should probably feel more list-y to the downstream MLP. And the attention mask is the same for all semantic information; it has to pay attention to the grammatical structure and the actual ‘vibes’ or meaning of the preceding text.

The fix seems pretty clear: just run a bunch of different attention mechanisms in parallel!

But then the question becomes: well our residual stream only takes things in \(R^{n \times d}\) so how do we actually wire this up?

One option is to just sum them, but then the output is just a fuzzy average of each head. What we really want is for the model to be able to ‘look at’ which head a given feature came from, and the feature index itself. This way the model can theoretically say “head 2 only tracks grammatical information so it shouldn’t push or pull on the sentiment dimension” (roughly speaking).

The shape that makes this work is:

\(\mathrm{MultiHead} = \mathrm{concat}(\mathrm{head}_1, \dots, \mathrm{head}_h)W_O\)

Where \(\mathrm{head}_i\) is the \(i^{th}\) attention ‘head’ and \(W_O \in \R^{hd \times d}\)

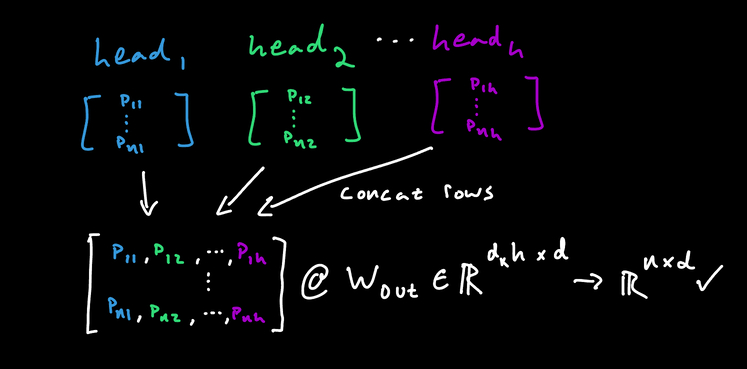
In code it looks like this:

# (n, d) x h -> concat -> (n, dh) @ (dh, d) -> (n, d)
class MultiHeadAttention(nn.Module):
    def __init__(self, n, d, h):
        super().__init__()
        self.heads = nn.ModuleList([Attention(n,d) for _ in range(h)])
        self.W_O = nn.Parameter(torch.randn(d * h, d) / math.sqrt(d))

    def forward(self, x: torch.Tensor):
        return torch.cat([h(x) for h in self.heads], dim=-1) @ self.W_O

And the results?

with these hyperparameters:

vocab_size = 2048
ctx_len = 32
batch_size = 4096
n_heads = 4
embedding_dim = 256
mlp_dh_coeff = 8
mlp_dh = embedding_dim * mlp_dh_coeff
mlp_depth = 2

Run on a 48mb dataset of high-quality gutenberg texts, the single-head model finishes with a validation perplexity of 67.68, and the multi-head version finishes with a validation perplexity of 66.48.

It’s not a massive difference, but it helps! Also note that i’m gpu poor so i’m running this on a small dataset with limited context. The results would likely be more striking on a larger set. Still an improvement!

The thing that’s most striking is the single head version shows an attention entropy of 1.177 at the end of training. The multi-head version has the following per-head attention entropies: [0.69, 0.158, 1.011, 0.861]

This is really interesting! One of the heads is nearly one-hot, and the others are fairly well-balanced. Clearly the different heads are doing different things. What are they doing exactly? We could look at the activations (intermediate model states) and see what’s lighting up, and which head attends to which tokens, but I’m going to leave that as an exercise for the reader. I might add a section later that looks at this once I’m using better models and more sensible hyperparameters.

For now, we just care that we pushed the test loss down. Great. Next.

dimension-reduced multi-head attention

The next thing to do is simply to push the attention mechanisms to work in a lower dimensional space.

Currently if a single head takes \(P\) parameters then a multi-head setup will take \(hP\) params. The question is: can we save some space by working in a lower dimensional space? In theory, if we’re using \(h\) heads, then each head has to care about fewer feature directions, and can do its job with a lower-dimensional representation. This means we get a smaller model which is nice.

The only thing to change is the shape of the attention weight matrices and the out projection: Just have them downproject to some \(d_k << d\)

# in Attention
self.W_Q = nn.Parameter(torch.randn(d,d_k) / self.sqrt_d)
self.W_K = nn.Parameter(torch.randn(d,d_k) / self.sqrt_d)
self.W_V = nn.Parameter(torch.randn(d,d_k) / self.sqrt_d)

# in MultiHeadAttention
self.W_O = nn.Parameter(torch.randn(d_k * h, d) / math.sqrt(d_k * h))

Also we need to choose some value for \(d_k\). If you cheat and look at the literature the way people do it is just set d_k = embedding_dim // n_heads. This way the number of parameters stays ~constant as we add more heads.

So does it work? Yes! We end up with a validation ppl of 65.11 which beats the full-rank multi-head attention and uses fewer parameters! It’s a little unexpected that we actually gain performance here. With such small models on such small datasets, we should take this with a grain of salt. The point is we’re not worse off doing this and we save a few parameters.

n-layer attention/mlp (transformers)

You already know what time it is. W’s in chat let’s stack some layers. I am not even going to bother really pedagogically motivating this. I mean come on. It’s so obvious. When we wanted more MLP performance we used a wider and deeper network. Since it’s not clear what a ‘wider’ multi-head attention setup looks like the only option is to go deeper.

Better yet, the change is trivial: we just do the embedding/positional encoding, then pass that through a bunch of multi-head attention/mlp blocks, then out with the W_out projection and we’re done. Each ‘block’ is just adding a new delta (recall, of shape \(\R^{n \times d}\)) to the residual stream.

class TransformerBlock(nn.Module):
    def __init__(self, n, d, h, d_k, mlp_dh, mlp_depth):
        super().__init__()
    
        self.attention = MultiHeadAttention(n,d,h,d_k)
        self.mlp = MLP(d, mlp_dh, mlp_depth)

    def forward(self, x: torch.Tensor):
        x = x + self.attention(x)
        return x + self.mlp(x)


class Transformer(nn.Module):
    def __init__(self, tokenizer, n, d, h, d_k, n_blocks, mlp_dh, mlp_depth):
        super().__init__()
        # ...
        self.W_pos = nn.Parameter(torch.randn(n, d))
        self.W_out = nn.Parameter(torch.randn(d, self.vocab_size) / math.sqrt(d))
        self.embedding = nn.Embedding(self.vocab_size, d)

        self.blocks = nn.Sequential(*[
            TransformerBlock(n, d, h, d_k, mlp_dh, mlp_depth)
            for _ in range(n_blocks)
        ])

    # x: (b, n) |-> (b, n, vocab_size)
    def forward(self, x: torch.Tensor):
        x = self.embedding(x) + self.W_pos  # (b,n) |-> (b,n,d)
        x = self.blocks(x)                  # (b,n,d) |-> (b,n,d)
        return x @ self.W_out               # (n d)(d vocab_size) = (n, vocab_size)

So how does it do? With 2 blocks, we get a final val perplexity of 55.74! Way better than the single block model. The training dynamics look a little sketchy, the first block’s attention masks are almost entirely one-hot by the end of training: [0.036, 0.013, 0.006, 0.01] but that’s not a big deal if the final val loss is down!

The generation quality is quite bad still, but it does look like we’re still marginally improving.

PROMPT:  ': in what circumstances then? must it not be in the most honourable? now such is death in war, because it is death in the'
OUTPUT:  'world, in which he has to do with that of a man who has been to the mind in his own nature, and as the predicate of a thing, and which is not so much as to think. It is a true cause. It is, that the whole in the United States are an objective reality, and is only in the mind (II. xiii.. and therefore (III. xi. not'

Now let’s try 4 blocks:

main | INFO | 2026-02-19 19:54:34 | starting training:
n_params=23.1M, n_batches=3548, batch_size=4096, context_length=33, tokens_per_batch=135.2K, total_tokens=1.4B
main | INFO | 2026-02-19 19:55:00 | {'batch': '100/3548', 'epoch': '1/3', 'tokens_seen': '13.5M', 'attn_entropy': {0: [nan, nan, nan, nan], 1: [nan, nan, nan, nan], 2: [nan, nan, nan, nan], 3: [nan, nan, nan, nan]}, 'batch_time_ms': 227.23, 'train_loss': nan, 'train_ppl': nan, 'val_loss': -inf, 'val_ppl': 0.0}

Shit.

RMSnorm

Well the attention masks are ‘blowing up’ again. Fortunately, we’ve seen this before. Recall the single-head attention post last time, when we tried doing attention without the \(\sqrt{d}\) scaling. What happened? The variance in the last dimension (ie per-row,per-position) was too high, and so one entry dominated the softmax, killed the gradient flow, and ruined our model. The fix was to normalize down to unit variance by dividing by the standard deviation.

Is the same thing happening here? Does the same fix work?

If we simply assume a mean of zero (it turns out that our residual stream does tend to center around zero), then the scaling factor is just:

\[\sqrt{\frac{1}{d}\sum_{i=1}^d x_i^2}\]

The right hand side is just there to illustrate that the scaling factor is roughly \(1\) (ie does little) if our input is already unit variance. The intuition is roughly:

\[\mathbb{E}[||x||_2^2] = \mathbb{E}\left[\sum_{i=1}^d x_i^2\right] = \sum_{i=1}^d \mathbb{E}[x_i^2] = \sum_{i=1}^d 1 = d \implies \mathbb{E}[||x||_2] \approx \sqrt{d}\]

Hence our scaling factor here is something like \(\sqrt{d}/\sqrt{d} = 1\)

In other words, if the residual stream is already nice, we’re not doing anything. If the residual stream has a huge variance, we’re normalizing it.

There are two remaining issues with this potential fix.

First, if \(x\) is near zero, we’re going to encounter numerical instability. The fix is to add some \(\varepsilon \approx 0.000001\) inside the square root.

Second, we’re adding inductive bias here. It’s true that we do not want high variance in our residual stream, but also we’re scaling it in a very particular way. To let the model choose how to re-scale after normalization, we can add an elementwise multiplication by some learned parameter \(\gamma \in \R^d\).

We call this ‘rescaling’ RMSnorm (root mean square) and the final form is this: \[ \mathrm{RMSnorm}(x) = \gamma \odot \frac{x}{\sqrt{\varepsilon + \frac{1}{d}\sum_{j=1}^d x_j^2}} \]

The operation is broadcasted across the rows of \(x\). We apply it not to the main residual stream, but to the inputs of each attention and MLP block.

In code:

class RMSNorm(nn.Module):
    def __init__(self, d):
        super().__init__()
        self.gamma = nn.Parameter(torch.ones(d))

    def forward(self, x: torch.Tensor):
        rms = torch.sqrt(torch.mean(x ** 2, dim=-1, keepdim=True) + 1e-6)
        return self.gamma * (x / rms) 

class TransformerBlock(nn.Module):
    def __init__(self, n, d, h, d_k, mlp_dh, mlp_depth):
        super().__init__()
    
        self.attention = MultiHeadAttention(n,d,h,d_k)
        self.mlp = MLP(d, mlp_dh, mlp_depth)
        self.rms1 = RMSNorm(d)
        self.rms2 = RMSNorm(d)

    def forward(self, x: torch.Tensor):
        x = x + self.attention(self.rms1(x))
        return x + self.mlp(self.rms2(x))

And the results are good! Running the network with this change gets us a validation ppl of 50.369 on the same set we’ve been using for a while now. In fact, this is the best we’ve managed to do!

And at this point… we have the transformer! It’s worth noting that the version we’re running here was the version that we’ve pieced together over the course of the post. This means we’re doing some ‘non-standard’ things. To name a few: still using vanilla SGD, using 3 layers in the MLP blocks, using RMSnorm before the attention/mlp blocks instead of e.g. layer norm after, probably using some suboptimal hyperparameters, (fairly arbitrary hidden size in the mlp), etc…

The reason for these changes from the Attention Is All You Need version is because it seemed more pedagogically tractable/honest to go this route.

Finally, there are (at least) two more obvious problems with the network, so i’ll leave it as an exercise to the reader to guess what they are and what we’re going to do about it in the next post. Maybe you can diagnose them from the log of the last training run:

main | INFO | 2026-02-20 20:33:34 | Sample generations (temperature = 0.5):
PROMPT:  'and the man who has lost all Self-Control, he that pursues excessive pleasures and too much avo'
OUTPUT:  'iding. His name was Man. He had a little late, whose cell was the most incidental of all the fashions of the damned, and the amount of the house. The porters were allowed to be considered as the various points of the other, and the garments of the kingdom. The men of the earth, the spoil of the people, and the'

main | INFO | 2026-02-20 20:33:36 | Sample generations (temperature = 0.0):
PROMPT:  'ming of these monsters, did display Past doubt her wisdom, taking from mad War Such slaves to do his'
OUTPUT:  'own. And now, as he was, he was a man of the most important matters, and he was not a man of the most important matters. He had not been able to be astonished, and he was not a man of the matter. He had not been a long time, but he had not been able to be in the least avoid. He had not been able to be in the least avoid.'

main | INFO | 2026-02-20 20:41:11 | {'batch': '3400/3548', 'epoch': '3/3', 'tokens_seen': '459.6M', 'attn_entropy': {0: [2.242, 2.243, 2.277, 1.515], 1: [0.855, 0.89, 1.004, 0.904], 2: [1.528, 1.332, 1.847, 1.545], 3: [1.516, 1.174, 1.976, 1.363]}, 'batch_time_ms': 294.81, 'train_loss': 3.311, 'train_ppl': 27.412, 'val_loss': 3.919, 'val_ppl': 50.369}
main | INFO | 2026-02-20 20:41:42 | gradient info:
    W_pos                               g=2.3e-02 w=9.0e+01 u=1.3e-05
    W_out                               g=4.3e-01 w=4.8e+01 u=4.5e-04
    embedding.weight                    g=2.2e-02 w=7.2e+02 u=1.5e-06
    blocks.0.attention.W_O              g=9.5e-02 w=1.4e+01 u=3.5e-04
    blocks.0.attention.heads.0.W_Q      g=7.1e-03 w=7.5e+00 u=4.7e-05
    blocks.0.attention.heads.0.W_K      g=7.1e-03 w=7.5e+00 u=4.8e-05
    blocks.0.attention.heads.0.W_V      g=5.2e-02 w=6.7e+00 u=3.9e-04
    blocks.0.attention.heads.1.W_Q      g=6.5e-03 w=7.5e+00 u=4.4e-05
    blocks.0.attention.heads.1.W_K      g=6.8e-03 w=7.5e+00 u=4.5e-05
    blocks.0.attention.heads.1.W_V      g=5.3e-02 w=6.8e+00 u=3.9e-04
    blocks.0.attention.heads.2.W_Q      g=6.3e-03 w=7.5e+00 u=4.2e-05
    blocks.0.attention.heads.2.W_K      g=6.7e-03 w=7.5e+00 u=4.5e-05
    blocks.0.attention.heads.2.W_V      g=4.9e-02 w=6.7e+00 u=3.6e-04
    blocks.0.attention.heads.3.W_Q      g=8.6e-03 w=7.8e+00 u=5.5e-05
    blocks.0.attention.heads.3.W_K      g=8.6e-03 w=7.8e+00 u=5.5e-05
    blocks.0.attention.heads.3.W_V      g=6.5e-02 w=6.8e+00 u=4.8e-04
    blocks.0.mlp.net.0.weight           g=2.4e-01 w=2.7e+01 u=4.4e-04
    blocks.0.mlp.net.0.bias             g=1.8e-02 w=1.8e+00 u=5.1e-04
    blocks.0.mlp.net.2.weight           g=4.3e-01 w=2.8e+01 u=7.6e-04
    blocks.0.mlp.net.2.bias             g=2.6e-02 w=6.0e-01 u=2.2e-03
    blocks.0.mlp.net.4.weight           g=5.1e-01 w=1.4e+01 u=1.8e-03
    blocks.0.mlp.net.4.bias             g=4.6e-02 w=2.7e-01 u=8.6e-03
    blocks.0.rms1.gamma                 g=8.7e-03 w=1.1e+01 u=3.9e-05
    blocks.0.rms2.gamma                 g=1.3e-02 w=1.8e+01 u=3.6e-05
    blocks.1.attention.W_O              g=2.3e-01 w=1.5e+01 u=7.5e-04
    blocks.1.attention.heads.0.W_Q      g=2.4e-02 w=8.2e+00 u=1.5e-04
    blocks.1.attention.heads.0.W_K      g=3.9e-02 w=8.1e+00 u=2.4e-04
    blocks.1.attention.heads.0.W_V      g=1.6e-01 w=7.9e+00 u=1.0e-03
    blocks.1.attention.heads.1.W_Q      g=2.3e-02 w=8.0e+00 u=1.4e-04
    blocks.1.attention.heads.1.W_K      g=4.1e-02 w=8.0e+00 u=2.6e-04
    blocks.1.attention.heads.1.W_V      g=1.7e-01 w=7.8e+00 u=1.1e-03
    blocks.1.attention.heads.2.W_Q      g=2.5e-02 w=8.0e+00 u=1.5e-04
    blocks.1.attention.heads.2.W_K      g=3.6e-02 w=8.1e+00 u=2.3e-04
    blocks.1.attention.heads.2.W_V      g=1.7e-01 w=7.8e+00 u=1.1e-03
    blocks.1.attention.heads.3.W_Q      g=2.6e-02 w=8.1e+00 u=1.6e-04
    blocks.1.attention.heads.3.W_K      g=4.5e-02 w=8.1e+00 u=2.8e-04
    blocks.1.attention.heads.3.W_V      g=1.6e-01 w=7.8e+00 u=1.0e-03
    blocks.1.mlp.net.0.weight           g=3.9e-01 w=3.1e+01 u=6.3e-04
    blocks.1.mlp.net.0.bias             g=4.4e-02 w=1.6e+00 u=1.3e-03
    blocks.1.mlp.net.2.weight           g=1.1e+00 w=3.3e+01 u=1.7e-03
    blocks.1.mlp.net.2.bias             g=5.7e-02 w=5.8e-01 u=4.9e-03
    blocks.1.mlp.net.4.weight           g=7.7e-01 w=2.0e+01 u=1.9e-03
    blocks.1.mlp.net.4.bias             g=6.7e-02 w=2.6e-01 u=1.3e-02
    blocks.1.rms1.gamma                 g=2.6e-02 w=1.5e+01 u=8.8e-05
    blocks.1.rms2.gamma                 g=1.5e-02 w=2.2e+01 u=3.5e-05
    blocks.2.attention.W_O              g=2.3e-01 w=1.4e+01 u=8.1e-04
    blocks.2.attention.heads.0.W_Q      g=2.6e-02 w=7.9e+00 u=1.7e-04
    blocks.2.attention.heads.0.W_K      g=3.9e-02 w=8.0e+00 u=2.4e-04
    blocks.2.attention.heads.0.W_V      g=2.0e-01 w=7.5e+00 u=1.4e-03
    blocks.2.attention.heads.1.W_Q      g=2.2e-02 w=8.0e+00 u=1.4e-04
    blocks.2.attention.heads.1.W_K      g=3.4e-02 w=8.1e+00 u=2.1e-04
    blocks.2.attention.heads.1.W_V      g=1.6e-01 w=7.6e+00 u=1.1e-03
    blocks.2.attention.heads.2.W_Q      g=2.4e-02 w=7.8e+00 u=1.5e-04
    blocks.2.attention.heads.2.W_K      g=4.6e-02 w=7.8e+00 u=2.9e-04
    blocks.2.attention.heads.2.W_V      g=2.3e-01 w=7.4e+00 u=1.6e-03
    blocks.2.attention.heads.3.W_Q      g=2.0e-02 w=8.1e+00 u=1.3e-04
    blocks.2.attention.heads.3.W_K      g=3.6e-02 w=8.1e+00 u=2.2e-04
    blocks.2.attention.heads.3.W_V      g=2.1e-01 w=7.5e+00 u=1.4e-03
    blocks.2.mlp.net.0.weight           g=3.4e-01 w=3.1e+01 u=5.6e-04
    blocks.2.mlp.net.0.bias             g=3.8e-02 w=1.6e+00 u=1.2e-03
    blocks.2.mlp.net.2.weight           g=9.3e-01 w=3.2e+01 u=1.4e-03
    blocks.2.mlp.net.2.bias             g=4.8e-02 w=5.8e-01 u=4.1e-03
    blocks.2.mlp.net.4.weight           g=6.4e-01 w=2.0e+01 u=1.6e-03
    blocks.2.mlp.net.4.bias             g=6.1e-02 w=2.8e-01 u=1.1e-02
    blocks.2.rms1.gamma                 g=3.2e-02 w=1.4e+01 u=1.2e-04
    blocks.2.rms2.gamma                 g=1.3e-02 w=2.2e+01 u=2.9e-05
    blocks.3.attention.W_O              g=2.3e-01 w=1.5e+01 u=7.6e-04
    blocks.3.attention.heads.0.W_Q      g=1.5e-02 w=7.9e+00 u=9.6e-05
    blocks.3.attention.heads.0.W_K      g=2.5e-02 w=8.0e+00 u=1.6e-04
    blocks.3.attention.heads.0.W_V      g=1.7e-01 w=7.6e+00 u=1.1e-03
    blocks.3.attention.heads.1.W_Q      g=1.8e-02 w=8.1e+00 u=1.1e-04
    blocks.3.attention.heads.1.W_K      g=3.0e-02 w=8.0e+00 u=1.9e-04
    blocks.3.attention.heads.1.W_V      g=1.5e-01 w=7.6e+00 u=1.0e-03
    blocks.3.attention.heads.2.W_Q      g=2.2e-02 w=7.9e+00 u=1.4e-04
    blocks.3.attention.heads.2.W_K      g=3.7e-02 w=7.9e+00 u=2.4e-04
    blocks.3.attention.heads.2.W_V      g=1.9e-01 w=7.7e+00 u=1.2e-03
    blocks.3.attention.heads.3.W_Q      g=1.8e-02 w=7.9e+00 u=1.2e-04
    blocks.3.attention.heads.3.W_K      g=2.6e-02 w=7.9e+00 u=1.7e-04
    blocks.3.attention.heads.3.W_V      g=1.8e-01 w=7.6e+00 u=1.2e-03
    blocks.3.mlp.net.0.weight           g=2.1e-01 w=3.2e+01 u=3.3e-04
    blocks.3.mlp.net.0.bias             g=1.9e-02 w=1.7e+00 u=5.7e-04
    blocks.3.mlp.net.2.weight           g=5.3e-01 w=3.2e+01 u=8.2e-04
    blocks.3.mlp.net.2.bias             g=2.2e-02 w=6.0e-01 u=1.8e-03
    blocks.3.mlp.net.4.weight           g=4.5e-01 w=2.1e+01 u=1.1e-03
    blocks.3.mlp.net.4.bias             g=2.1e-02 w=3.3e-01 u=3.2e-03
    blocks.3.rms1.gamma                 g=3.1e-02 w=1.4e+01 u=1.1e-04
    blocks.3.rms2.gamma                 g=1.3e-02 w=2.4e+01 u=2.8e-05
main | INFO | 2026-02-20 20:41:42 | {'batch': '3500/3548', 'epoch': '3/3', 'tokens_seen': '473.1M', 'attn_entropy': {0: [2.242, 2.243, 2.276, 1.506], 1: [0.859, 0.895, 1.008, 0.907], 2: [1.533, 1.323, 1.849, 1.558], 3: [1.506, 1.182, 1.986, 1.392]}, 'batch_time_ms': 289.84, 'train_loss': 3.331, 'train_ppl': 27.968, 'val_loss': 3.919, 'val_ppl': 50.369}
main | INFO | 2026-02-20 20:42:17 | training finished w/ final val ppl=48.66081389514648